Paper • 2023-09-28 16:12:13

論文紹介「スペクトログラム相互相関で鳥の鳴き声の複雑さを計測できる（Suyash,2021）」

「鳥の鳴き声の複雑さ」としてSPCC（スペクトログラム相互相関）を用いた指標(NVI)を導入し、他の手法からの有効性を示しています。特にノートのスペクトログラム内の変化の変異度についても取り扱えると主張しています。

論文を読んだのでその備忘録です。せっかくなので共有します。

論文

スペクトログラム相互相関(SPCC)で鳥の鳴き声の複雑さを計測できる

Spectrogram cross-correlation can be used to measure the complexity of bird vocalizations

インド科学教育研究研究所 (IISER) 生物学部、ティルパティ、ティルパティ、インド

Suyash Sawant, Chiti Arvind, Viral Joshi, V. V. Robin

First published: 12 November 2021

この論文のポイント

SPCC(Spectrogram cross-correlation)を用いてノート変異指標(NVI: Note Variability Index)を提案。
SPCC は、各音符のオーディオファイルのスペクトログラム間のピクセル間のマッチングを使用し、相関係数 $C_{Δ t}$ が計算される。
NVIは以前に使用されていた曲の複雑さの尺度では不可能だった複雑さを定量化しながら、ノート内のスペクトルの違いを考慮できる
NDI:Note Diversity Index と SH:Shannon’s Equitabilityはノート内の音響変化を考慮せず、ノートを手動で分類する必要があるため、正確で無く、処理が難しく、計算速度が遅い。同じ構造の曲の場合、音符が別個の単位としてのみ考慮され、バリエーションの程度は考慮されないため、NDI と SH はまったく同じ複雑さの値を与える。
NVIを適切に得るには音源が高品質 (SNR > 10 dB)であること
NVIはSPCCだけでなく様々なスペクトログラム相関を用いることができる

概要（google 翻訳）

鳥の鳴き声は、配偶者を引き寄せたり、縄張りを守るための重要な合図です。これらの曲の複雑さを定量化することで、個人のフィットネス、性的選択、行動を明らかにすることができます。曲の複雑さを定量化するためにいくつかの手法が使用されており、それらは連続的なバリエーションの尺度と多様性の尺度に大別されます。ただし、これらの方法では、周波数帯域幅や、ボーカル信号の不可欠な部分であるノートのスペクトル時間形状の多様性などの重要な音響特徴を説明できません。この研究では、鳴き声内の音符の変動を考慮し、スペクトル相互相関を使用して鳥の鳴き声の加重指数を計算する新しい複雑さの方法を提案します。
まず、以前に説明した方法を比較して、曲の複雑さに影響を与える要因に基づいてその利点と制限を理解しました。次に、音符のスペクトル特徴を組み込んで複雑さを定量化する新しい手法である音符変動指数 (NVI) を開発しました。この方法により、間違いが発生しやすいメモを手動で分類する必要性が軽減されます。スペクトログラム相互相関を使用して曲内のノートを比較し、出力値を使用して曲の複雑さを定量化しました。
新しい方法の有効性を評価するために、極端な曲の複雑さを風刺する合成曲を生成し、選択した従来の複雑さの方法を NVI と比較しました。これらのメソッドにはケース固有の制限が設けられています。さらに、現実世界のシナリオにおけるこの新しい手法の有効性を検証するために、さまざまな構造を持つ世界中の複数の種の自然の鳥の鳴き声を使用して、従来の手法と NVI を比較しました。
私たちの知る限り、NVI は、従来の方法では異なる音符タイプを持つ類似した曲構造を区別できない、曲中の音符の分光時間的形状の変化を捉える唯一の曲複雑性手法です。さらに、NVI は音符を手動で分類する必要がないため、既存の音分析ソフトウェアを使用してあらゆる種類の鳥の鳴き声に対して簡単に実装できます。これは迅速であり、メモ分類における主観性の可能性を回避し、大規模なデータセットに対して自動化することができます。

内容

さえずりの複雑さを定量化する同等の方法は課題として残っている（Kershenbaum & Garland, 2015; Mikula et al.）
鳥のさえずりの複雑さの特徴：
- 1. 即時的:個々の歌の複雑さ
- 1. 最終的:歌全体にわたる複雑さ (Garamszegi et al., 2005 )
メスは選択をする前にオスのレパートリー全体ではなく、少数の歌を聞く可能性が高いため、即時の歌の複雑さは配偶者の選択により関連します (Garamszegi et al., 2012 )
これまでの研究では、鳥のさえずりの複雑さを、多様性、繰り返し、順序、音符の組み合わせ、およびその伝達率に基づいて測定：
1. Order of notes：
  1. マルコフモデル（曲内の音符の遷移確率）、Lempel-Ziv 複雑さ、レーベンシュタイン距離、エントロピー率、歌内の音符の順序
  2. スペクトルパラメータが考慮されていないため、音符の構造的多様性という観点から曲の複雑さを必ずしも説明できるわけでない
2. Diversity of notes：
  1. 曲内のノートの定常確率を使用して定量化。シャノンの多様性は、音符の定常確率を測定することによって相対的な存在量を使用して、曲の複雑さを定量化
  2. レパートリーサイズは最終的な音の多様性を捉えていますが、より大きなレパートリーのサイズを持つ鳥は歌の中で同じ音を繰り返す可能性があり(即時的な多様性が低い、例えばキツネドリ)、限られた音符を持つ鳥は歌の中の複雑さを表していない可能性がある
  3. レパートリーによっては、非常に少ない音符の組み合わせから複雑な歌を作成する場合がある (例: ハイイロカナリア、ヒタキ)。
  4. その他、曲内の音符の数、曲内の音符の種類、または音符の種類と音符の数の比率
  5. リピート分布と相互情報量はより複雑でレアなノートの発生が組み込まれるが、曲のスペクトル特性の範囲は考慮されていない
  6. ノートを個別のタイプに手動で分類する必要がある
3. Spectral parameters based：
  1. 最小値と最大値 (周波数と時間) のみが考慮されるため、音符のスペクトログラムの時間形状が失われる

提案方法： Note Variability Index (NVI)

$N_C$ 個の音符がある曲では、正規化された相関係数 $C_{Δt}∈ (0, 1)$ は、音符の各ペアを相関させることによって取得され、 $N_C × N_{C}$ の類似度行列を形成します。1 に向かう傾向のある $C_{Δt}$ 値は 2 つのノート間の関連性が高いことを表し、 $C_{Δt} = 0$ はノート間に関連性がないことを意味します。

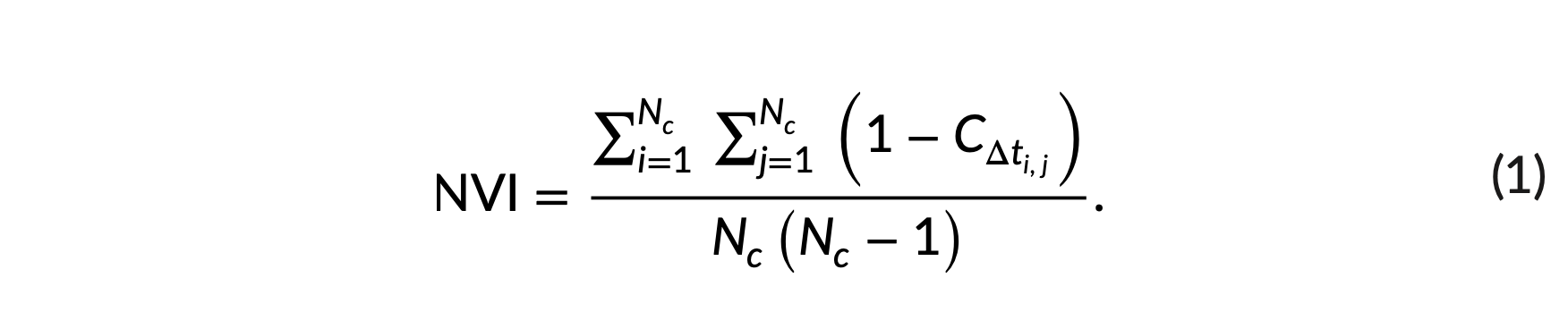
NVI は、類似度行列 $(1 − C_{Δt})$ の逆相関係数の累積スコアです。ここで、 $i$ と $j$ は行と列のランクです。分母 $N_c ( N_c − 1)$ は、音符の数が異なる曲間で曲の複雑さを比較するための正規化された値を取得するために使用されます。
NVI ∈ (0, 1) の出力値 (式 1)。値が大きいほど複雑性が高いことを表し、値が小さいほど複雑性が低いことを表します。

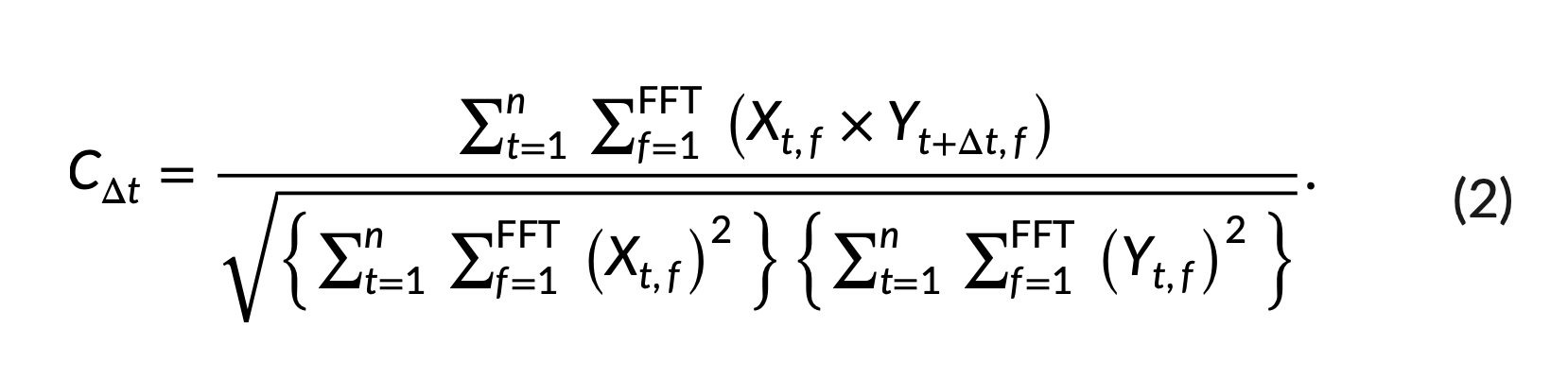
この研究では、ソフトウェア Raven Pro 1.5 の「Batch Correlator」機能に実装された SPCC を使用して $C_{Δt}$ を計算しました
SPCC は、各音符のオーディオファイルのスペクトログラム間のピクセル間のマッチングを使用し、相関係数 $C_{Δ t}$ が計算されます (式 2)。ここで、 $n = N_1 + N_2 − 1$ 。 $N_1$ 、 $N_2$ は 2 つのスペクトログラムのフレーム数、 $FFT$ は周波数ビンの数、 $X_t$ 、 $f$ 、 $Y_t$ 、 $f$ は時間 $t$ および周波数 $f$ における 2 つのスペクトログラムの振幅値です。この研究における（各曲の）すべてのノートの相関係数データは、データに同じスペクトルパラメーターを使用し、Hann スペクトログラムウィンドウサイズ 512、50% のオーバーラップ、および DFT を使用して、Raven Pro の「Batch Correlator」を通じて取得されました。サイズは512です。

NVIと従来との比較

人工合成音で比較
曲の複雑さを定量化するために広く使用されている次の 2 つの尺度を使用:
- 1. NDI:音符タイプと音符数の比率 ( $N_T / N_C$ )
- 1. Shannon’s equitability: $N_T$ 音符タイプ、 $N_C$ は音符の総数を表し、 $p_i$ は曲内の各音符の定常確率を表します。

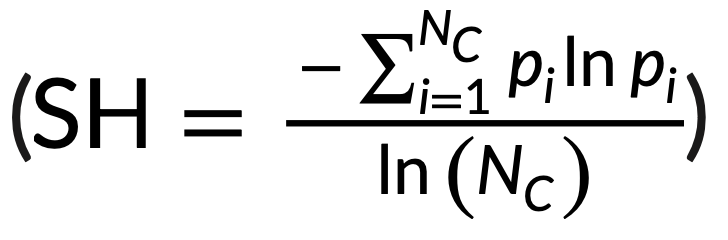
曲の複雑さを説明する際に最近使用された平均周波数 (Hz)、周波数帯域幅 (Hz)、継続時間 (s) などの 3 つの音響パラメーターを使用して、これらの測定値を機能的多様性測定値 (FRic、FEve、FDiv) と比較しました

実際の鳥のさえずりの音の変動指数

世界のさまざまな地域から選択した 15 種の自然の鳥のさえずりを使用
複雑なさえずりを持つと考えられる鳥類 6 種を最終候補リストに挙げました。
- キツネドリ類 Toxostoma rufum (Boughey & Thompson、1981 年)、
- ナイチンゲール Luscinia megarhynchos
- キタマネシドリMimus Polyglottos
- ソングツグミTurdus philomelos
- シロハラショラキリSholicola albiventris
- シロカンムリスズメZonotrichia leucophrys
可変音次数とスペクトルパラメータを持つさえずりを持つ9種を選択
- チャバラマユミソサザイThryothorus ludovicianus、
- ハイガシラヒタキCulicicapa ceylonensis、
- ズグロヤイロチョウPitta Sordida、
- セグロカッコウCuculus micropterus、
- チビメジロハエトリEmpidonax minimus
- ショウジョウコウカンチョウCardinalis Cardinalis、
- シキチョウCopsychus saularis、
- アカメモズモドキVireo olivaceus
- チャガシラゴシキドリMegalaima viridis。
マコーレー図書館（コーネル大学）から 14 種の歌の録音を入手し、私たちの研究室のシロハラショラキリの録音を使用しました。それぞれの別々の録音が異なる鳥の個体からのものであると仮定して、種ごとに 10 個体の歌を収集し、分析のために個体/録音ごとに 10 の歌を選択しました。これにより、種ごとに合計 100 曲のデータセットが作成されました。録音と曲は、録音品質と、ほとんどの場合 15 dB 以上の SNR に基づいて選択されました。すべての曲は、Raven Pro の 1 人 (SS) によって手動で注釈が付けられました。

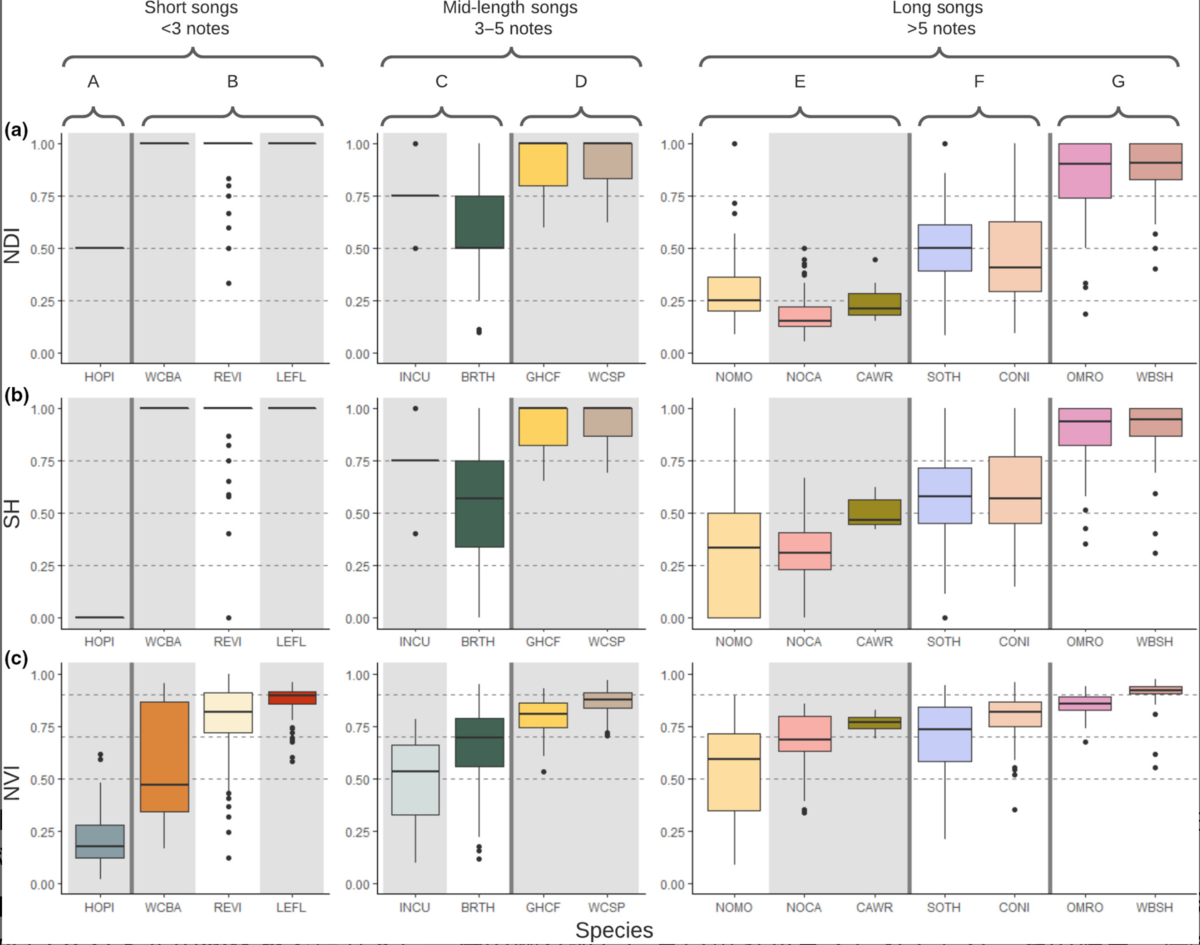
NDI と SH は、可変音符を含む長い曲の多様性を捉えるが、スペクトルの多様性が低い音符タイプ (例: アカガシラビレオ、ハイイロカナリアビタキ、シロホオビタキ) を持つ短い曲の場合の複雑さの値を過大評価
周波数やスペクトルの変化を考慮せずに音符の繰り返しに高い重みが与えられており、複雑さが過小評価 (例: モッキンバード、キタコアジナル、カロライナミソサザイ; 図2a、b )。
即時音の多様性に関する NVI は、複雑さを推定しながらスペクトルの多様性を説明 (図 2c )。これにより、周波数帯域幅が非常に狭い種 (インドカッコウやホオジロゴシキなど) の複雑さの値が比較的低くなる。NVI は、スペクトル変化が大きいいくつかの音の繰り返しを持つ歌を持つ種 (モッキンバード、キタコウカンドリ、カロライナミソサザイなど) の場合、比較的高い複雑さの値を与える。
曲全体の全体的な多様性を推定するために NVI を使用した場合、曲全体でノートのスペクトル変化が大きい非定型的な曲 (例: ソングツグミ、ブラウンツグミ、モッキンバードなど) では、場合によっては複雑さのより高い値が予測されました。一方、似たような音が歌の間で繰り返される常同的な歌を持つ鳥の場合、全体的な種類の NVI 値は直接のものよりも相対的に低くなります (例:インドカッコウ、ホオジロゴシキドリ、キビタキ) (図 3 )。

NVI計算の代替方法

NVI は、ノート間の類似性を定量化できる他のツールを使用して計算することもできる
スペクトログラム相関を使用分類方法：
- ピアソンの相関、スピアマンの順位相関、ケンダルの順位相関 (Hauke & Kossowski, 2011 ) があり、「 warble R」パッケージを使用して簡単に実装できます(Araya-Salas & Smith-Vidaurre, 2017 )。
- 周波数等高線の動的タイムワーピング (DTW) (Daniel Meliza et al., 2013 ; Kaewtip et al., 2016 )、
- Soundpoints (Taft, 2011))、
- 特徴ベースの分類 (Greig & Webster、 2013 )、
- 隠れマルコフモデル (Kaewtip et al.、 2016 )、
- 畳み込みニューラルネットワークなどのいくつかの深層学習手法 (Narasimhan et al.、 2017 ) も音響信号の分類に広く使用されています。
曲内のノートのタイプに基づいて、これらの方法のいくつかを使用して NVI を計算すると、より堅牢な複雑さの値を得ることができます。たとえば、強い倍音や近接した倍音が存在しない調性ノートを含む曲の場合、周波数等高線の DTW はより多くの特徴を効率的にキャプチャでき、その結果、複雑さの堅牢な測定が得られます。
これらの可能性のいくつかを評価しましたが、使いやすさと種を超えた幅広い適用性を考慮して、Raven Pro に実装されている SPCC を使用することにしました。

用語

歌は目に見える時間のギャップによって区切られた一連のノートと音節を指す。
ノートは曲の最小単位
Lempel-Ziv complexity LZ の複雑さは、特定のシーケンスの多様性または独自性を定量化します。これは、シーケンスを圧縮し、元のシーケンスと比較して圧縮された表現の長さを測定することによって機能します。
レーベンシュタイン距離（レーベンシュタインきょり、英: Levenshtein distance）は、二つの文字列がどの程度異なっているかを示す距離の一種である。編集距離（へんしゅうきょり、英: edit distance）とも呼ばれる。具体的には、1文字の挿入・削除・置換によって、一方の文字列をもう一方の文字列に変形するのに必要な手順の最小回数として定義される。
エントロピーレート 確率の数理理論において確率過程における情報量の時間平均である。

以上